شناخت مسائل NP, NP-Hard & NP-Complete
آشنایی با نظریه NP در طراحی الگوریتم
نظریه NP (نظریه پیچیدگی محاسباتی) شاخهای از نظریه محاسبات و ریاضی و علوم کامپیوتری است که به بررسی دشواری حل مسائل بهصورت الگوریتمی میپردازد. برای آشنایی با این نظریه بهتر است ابتدا مفاهیمی را تعریف کنیم:
مسائل تصمیمپذیر و تصمیمناپذیر:
در تئوری محاسبات مسایل تصمیمگیری به دو دسته تصمیمپذیر و تصمیمناپذیر تقسیم میشوند. یک مسئله تصمیمپذیر مسئلهای است که قابل حل باشد به این معنی که بتوان یک الگوریتم برای آن طراحی کرد، در غیر این صورت مسئله مورد نظر تصمیمناپذیر خواهد بود.
مسایل تصمیمپذیر به نوبه خود و با توجه به مرتبه زمانی حل خود به دستههای متفاوتی تقسیم میشوند. دستهای از آنها مسایلی هستند که برای آنها الگوریتمی با مرتبه زمانی چند جملهای موجود میباشد. این مسایل به کلاس مرتبه زمانی P تعلق دارند. از طرف دیگر مسایلی وجود دارند که اثبات شده است الگوریتمی با مرتبه زمانی چند جملهای برای آنها وجود ندارد. همچنین مسایلی وجود دارند که تعلق یا عدم تعلق آنها به کلاس P اثبات نشده است. تمام مسایل NP-Complete و برخی از مسایل NP-Hard از این دسته مسایل میباشند.
تمام مسایل NP-Complete به طور موثری قابل کاهش به یکدیگر میباشند. بنابراین اگر یکی از آنها با یک مرتبه زمانی چند جملهای بر حسب اندازه مسئله حل شود، تمامی آنها با این مرتبه زمانی قابل حل خواهند بود.
کلاس NP-Hard شامل بسیاری از مسایل بهینهسازی از جمله مسئله Max-SAT میباشد، که این مسئله گونه بهینهسازی مسئله ارضاءپذیری میباشد.
مسائل بغرنج Intractable
الگوریتم زمانی چندجملهای، الگوریتمی است که در بدترین حالت پیچیدگی زمانی آن تابع چندجملهای از اندازه ورودی باشد. مسئلهای بغرنج است که حل آن توسط الگوریتمی بازمان چندجملهای غیرممکن باشد. بحث ما بر سرخود مسئله است و نه الگوریتم حل مسئله. ممکن است برای حل مسئله الگوریتمهای متعددی بازمان های مختلف وجود داشته باشد؛ مثلاً حل مسئلهی سری فیبوناچی با روش تقسیم و حل از مرتبه نمایی و با روش پویا از مرتبه خطی است، پس مسئله فیبوناچی از نوع بغرنج نیست.
برای آنکه مسئلهای بغرنج باشد باید اثبات کرد که هیچ الگوریتمی با مرتبه چندجملهای برای آن وجود ندارد. ازنظر بغرنج بودن یا نبودن، مسائل علوم کامپیوتر سه دسته هستند:
- مسائلی که الگوریتمهایی با پیچیدگی زمانی چندجملهای برای آنها پیداشده است.
- مسائلی که اثباتشده است که بغرنج هستند، یعنی الگوریتم چندجملهای برای آن یافت نمیشود.
- مسائلی که بغرنج بودن آنها ثابت نشده است ولی از طرف دیگر هیچ الگوریتم چندجملهای هم برای آنها پیدا نشده است.
مثلاً جستوجوی دودویی در آرایه مرتب با مرتبه زمانی θ(logn)، مسئله مرتبسازی آرایهها با مرتبه زمانی θ(nlogn)، ضرب زنجیرهای ماتریسها با مرتبه زمانی θ(n3) از دسته اول هستند. همچنین مسائل کوتاهترین مسیر فلوید با مرتبه زمانی θ(n3)، درخت دودویی بهینه θ(n3) و مسئله درخت پوشای کمینه پریم θ(n2) بااینکه الگوریتمهای نمایی نیز دارند ولی چون برای آنها الگوریتمهایی از نوع چندجملهای یافت شده است از این دستهاند.
تعداد مسائلی که جزو دسته دوم بوده و بغرنج بودن آنها اثباتشده است، نسبتاً کم بوده است. نمونهای از این مسائل دسته دوم، حساب پرزبرگر است.
مسئله کولهپشتی صفر و یک و مسئله فروشنده دورهگرد از دسته سوم هستند.
رابطه مسائل بهینهسازی با مسائل تصمیمگیری
خروجی مسائل بهینهسازی یک حل بهینه است و خروجی مسائل تصمیمگیری جواب بله یا خیر است. هر مسئله بهینهسازی را میتوان متناظر با یک مسئله تصمیمگیری در نظر گرفت. پس در ادامه روی مسائل تصمیمگیری بهجای مسائل بهینهسازی تمرکز میکنیم:
کلاس P
بهطورکلی مسائل تصمیمگیری را به چهار کلاس تقسیم میکنیم. مسائلی که برای حل آنها الگوریتم یا الگوریتمهایی با مرتبه زمانی چندجملهای یافت شده است کلاس الگوریتمهای معین یا الگوریتمهای قطعی را تشکیل میدهند. این کلاس را با علامت ویژه p که کوتاه شده polynomial به معنای چندجملهای هست نمایش میدهیم.
الگوریتمهایی که برای کامپیوترهای رایج طراحی میگردند الگوریتمهای معین نامیده میشوند. در این الگوریتمها نتیجه هر عمل کاملاً مشخص، معین و قطعی است. P کلاس کلیه مسائل تصمیمگیری است که برای حل آنها الگوریتم معین با مرتبه زمانی چندجملهای وجود دارد.
کلاس NP
NP مخفف “Non-Deterministic Polynomial” یکی از سادهترین و بنیادیترین کلاسهای پیچیدگی در تئوری پیچیدگی در نظریه زبان محسوب میشود. اساساً NP شامل تمام مسائل تصمیمگیری میشود که در آنها خروجی مثبت به معنی اثبات شدن درستی یک حقیقت است و پیدا کردن جواب بله برای آنها شامل اثبات ساده ای است که جواب حقیقتاً باید بله باشد.
بهطور دقیقتر، این اثباتها باید در زمان چندجملهای با استفاده از یک ماشین قطعی تورینگ قابل تصدیق شدن باشند. در تعریفی مشابه گفته میشود که NP مجموعهی مسائل تصمیمگیری است که در زمان چندجملهای و با استفاده از ماشین غیرقطعی تورینگ قابلحل شدن هستند. کلاس پیچیدگی P یکی از اعضای NP است اما NP شامل کلاسهای مهم دیگری نیز هست. که پیچیدهترین آنها NP-Complete است بطوریکه برای آنها هیچ الگوریتم شناخته شده قابل اجرا در زمان چند جمله ای وجود ندارد .
مهمترین سوالی که اکنون برای این کلاسها در این نظریه وجود دارد این است که آیا P=NP؟ این سوال می پرسد که آیا چنین الگوریتمی واقعاً برای مسائل NP-Complete و در کل NP وجود دارد یا خیر. این باور گسترده وجود دارد که این تساوی نمیتواند درست باشد.
برای معرفی کلاس NP باید با مشخصات ماشین غیر قطعی تورینگ آشنا شویم. ماشینی را تصور کنید که افزون بر توانایی اجرای دستورهای معین و قطعی قادر است برخی دستورهای غیرقطعی را نیز اجرا کند. یک دستور غیرقطعی دستوری است که نتیجه اجرای آن از قبل قابل پیشبینی نیست. الگوریتمهایی که برای یک کامپیوتر غیرقطعی طراحی میشوند الگوریتمهای غیرقطعی نامیده میشوند. برای بیان اینگونه الگوریتمها افزون بر دستورهایی که برای بیان الگوریتمهای قطعی وجود دارد از سه تابع زیر استفاده خواهیم کرد:
choice(S)
این تابع یکی از عناصر مجموعه S را بهدلخواه انتخاب میکند. عمل انتخاب برای یک کامپیوتر غیرقطعی عمل سادهای است.
failure()
این تابع پایان ناموفق عملیات الگوریتم را اعلام میکند. این اعلام به مفهوم جواب false برای مسئله تصمیمگیری موردنظر هست.
success()
این تابع پایان موفق عملیات الگوریتم را اعلام میکند. این اعلام به مفهوم جواب true برای مسئله تصمیمگیری موردنظر است.
تشخیص اول یا اول نبودن یک عدد طبیعی، مرتب کردن اطلاعات و ارضاء پذیری نمونههایی از مسائلی هستند که میتوان الگوریتمهای غیرقطعی سادهای برایشان طراحی کرد.
در بیان یک الگوریتم غیرقطعی ممکن است از همه دستورها و بهویژه از دستورهای choice، failure و success استفاده نشود؛ بنابراین هر الگوریتم معین توسط یک کامپیوتر غیرقطعی قابلاجرا است. پس P زیرمجموعه NP است. محققین زیادی سعی کردهاند ثابت کنند P = NP اگر این مسئله ثابت شود مفهوم آن این است که هر مسئلهای که برای آن الگوریتم غیرقطعی با مرتبه زمانی چندجملهای وجود دارد میتوان برای آن یک الگوریتم معین با مرتبه زمانی چندجملهای نیز پیدا کرد.
یکی از مسائل عضو کلاس NP مسئله ارضاء پذیری (Satisfiability) است. مسئله ارضاء پذیری بررسی این مطلب است که آیا یک عبارت منطقی داده شده به ازای مقادیری از لفظهای تشکیلدهنده آن درست خواهد بود. طراحی یک الگوریتم غیرقطعی که تشخیص بدهد یک عبارت داده شده صدق پذیر است یا خیر مشکل نیست.
در سال 1971، S.A. Cook ثابت کرد که چنانچه ثابت شود که ارضاء پذیری به کلاس P تعلق دارد، آنگاه P = NP است و بالعکس. با بیان این مطلب مسئله ارضاء پذیری از اهمیت بالایی برخوردار میشود، بهگونهای که کلاسهای NP-Hard و NP-Complete بر محور این قضیه شکل میگیرند. افزون بر آن تلاش دانشمندانی را که در مسیر اثبات P = NP فعالیت میکنند جهتدار مینماید و فعالیت آنها را حول محور تلاش برای یافتن راهحل معین چندجملهای برای مسئله ارضاء پذیری متمرکز میکند.

از مهمترین مسائل کلاس NP میتوان به مسئله فروشنده دورهگرد (Salesman Problem)، تجزیه اعداد صحیح (Integer Factorization) و همریختی گرافها (Graph Isomorphism) اشاره کرد.
کلاس NP-hard
ریشهٔ انگلیسی ان پی-سخت: (NP-hard→Non-deterministic Polynomial-time hard) به معنای حل نشدنی درزمان چندجملهای بر حسب اندازهٔ ورودی مساله (زمان معقول)
مجموعهٔ «انپی-سخت» شامل چندهزار مسالهٔ مختلف با کاربردهای فراوان است که تاکنون برای آنها راه حل سریع و قابل انجام در زمان معقول پیدا نشدهاست و به احتمال زیاد در آینده نیز یافت نخواهد شد. این که راه حل سریعی برای آنها وجود ندارد هم اثبات شدهاست. البته ثابت شدهاست که اگر فقط برای یکی از این مسالهها راه حل سریعی پیدا شود؛ این راه حل موجب حل سریع بقیهٔ مسالهها خواهد شد. البته احتمال پیدا شدن چنین الگوریتمی ضعیف است. منظور از راه حل سریع آن است که زمان اجرای آن با اندازهٔ ورودی مساله به صورت چندجملهای رابطه داشته باشد.
برای درک مسائل ابتدا مفهوم کاهش پذیری بین مسائل را تعریف میکنیم.
فرض کنید M1 و M2 دو مسئله باشند. مسئله M1 به مسئله M2 کاهش پیدا میکند (M2 → M1 ) اگر و فقط اگر چنانچه یک الگوریتم معین با مرتبه زمانی چندجملهای برای M2 وجود داشته باشد، آنگاه بتوان با به کارگیری الگوریتم معین با مرتبه زمانی چندجملهای که M2 را حل میکند، M1 را با الگوریتمی معین و زمان چندجملهای حل کرد. رابطه کاهش پذیری یک رابطه با خاصیت تعدی است یعنی اگر M1 → M2 و M2 → M3 آنگاه: M1 → M3.
مسئله M یک مسئله NP-hard است اگر و فقط اگر ارضاء پذیری به آن کاهش پیدا کند (Satisfiability→M).
کلاس NP-hard تنها به مسائل تصمیمگیری محدود نمیشود. نمونهای از مسائل NP-hard که درعینحال NP-complete نیست «مسئله توقفپذیری» است. در این مسئله هدف ساختن الگوریتمی است که مشخص کند آیا یک برنامه کامپیوتری داده شده هیچوقت پایان خواهد یافت (اجزای آن تکمیل خواهد شد و توقف خواهد کرد و یا وارد حلقه نامتناهی خواهد گردید). ورودی چنین الگوریتمی میتواند هر برنامه کامپیوتری و طیف دادههای آن باشد و خروجی چنین الگوریتمی بله یا خیر است. بله یعنی اینکه برنامه ورودی توقف خواهد کرد و خیر یعنی برنامه ورودی در حلقهای نامتناهی گیر خواهد افتاد. الگوریتمی که برای هر برنامه ورودی و طیف دادههای آن جواب درستی بدهد محاسبهناپذیر است، یعنی هیچ راهحل الگوریتمی برای آن وجود ندارد. نتیجه اینکه «مسئله توقفپذیری» به کلاس NP تعلق ندارد.
معروفترین مسائل ان پی-سخت:
- مسئله فروشنده دورهگرد
- مسئله بزرگترین خوشه (پیدا کردن بزرگترین زیرگراف کامل) (maximum clique problem)
کلاس NP-complete
مفهوم NP-Complete برای اولین بار در سال ۱۹۷۱ توسط Stephen Cook در مقالهای با عنوان «پیچیدگی تئوری اثبات رویهها» معرفی شد؛ اما نکته جالب اینجاست که خود عبارت NP-Complete در هیچ جای مقاله استفادهنشده بود. در آن کنفرانس علوم کامپیوتر بحث و مناظره شدیدی بین دانشمندان علوم کامپیوتر بر سر اینکه آیا مسائل NP-Complete میتوانند در یک پیچیدگی زمانی چندجملهای توسط ماشین تورینگ قطعی حل شوند یا نه درگرفت.
در آن کنفرانس آقای John Hopcroft همهی اعضا را با توجه به اینکه هیچکس اثبات رسمی برای ادعای خود نداشت، به این توافق رساند که این سؤال را که آیا مسائل NP-Complete در پیچیدگی زمانی چندجملهای قابلحل هستند یا نه را به زمان دیگری موکول کنند. از آن زمان تاکنون هنوز هیچ فردی نتوانسته بهطور قاطعانه ادعا کند که آیا مسائل NP-Complete در پیچیدگی زمانی چندجملهای قابل هستند یا نه؟ و این موضوع به یکی از بزرگترین مسائل حلنشدهی ریاضیات تبدیلشده است.
موسسه ریاضیات Clay پیشنهاد پاداش یک میلیون دلاری برای کسی که یک اثبات رسمی مبنی بر اینکه آیا P=NP یا P≠NP ارائه کند را داده است.
در تئوری پیچیدگی محاسباتی، کلاس پیچیدگی NP-Complete (بهطور خلاصه NPC)، یکی از کلاسهای مسائل تصمیمگیری است. یک مسئله تصمیمگیری مانند L یک مسئله NP-Complete است اگر در مجموعهی مسائل NP باشد بهطوریکه هر راهحلی که برای مسئلهی تصمیمگیری میدهد دارای پیچیدگی زمانی چندجملهای یا O(nk) باشد. همچنین میتوان این مسئله را در حوزه NP-Hard نیز در نظر گرفت اگر بتوان هر مسئله NP را با تغییر ورودی به L تبدیل کرد.
برای نشان دادن اینکه آیا یک مسئله NPC است یا نه از سه مفهوم کلیدی استفاده میکنیم: مسائل تصمیمگیری در مقابل مسائل بهینهسازی و دیگری کاهش
توضیح در مورد دو مفهوم مسائل تصمیم گیری و بهینه سازی
بسیاری از مسائل موردعلاقهی ما مسائل بهینهسازی هستند که در آنها به هر یک از راهحلهای محتمل یک مقدار میدهیم و تلاش میکنیم راهحلی را با بهترین مقدار پیدا کنیم. برای مثال مسئلهی «کوتاهترین مسیر» گراف بدون جهت G را داریم و میخواهیم مسیری از رأس u تا v را پیدا کنیم که شامل کمترین لبهها باشد.
در نظریه شمارش و همچنین پیچیدگی محاسباتی، مساله تصمیم گیری، سوالی با پاسخ بله یا خیر میباشد که به ورودی بستگی دارد.
NPC بودن بهطور مستقیم در مسائل بهینهسازی به کار نمیرود بلکه در مسائل تصمیمگیری که در آنها جواب بله یا خیر است (بهطور رسمی صفر یا یک) است به کار میرود. بنابراین نشان دادن اینکه مسئلهای NPC است یا نه ما را به ناحیه مسائل تصمیمگیری محدود میکند. جایی که ارتباط مناسبی بین مسائل بهینهسازی و تصمیمگیری وجود دارد.
ما معمولاً میتوانیم یک مسئلهی بهینهسازی رو با محدود کردن مقدار بهینه به شکل یک مسئلهی تصمیمگیری درآوریم. بهعنوانمثال در مسئلهی کوتاهترین مسیر گراف بدون جهت G مقدار k به عنوان حد تعیین می شود و مسئله تصمیم گیری به این شکل بیان می شود: آیا مسیری بین دو رأس u و v وجود دارد که لبه های آن کمتر یا مساوی k باشد؟
ارتباط بین مسئلهی بهینهسازی و مسئلهی تصمیمگیری زمانی به درد میخورد که بخواهیم نشان دهیم مسئلهی بهینهسازی موردبحث یک مسئلهی سخت (hard) است. این به این خاطر است که مسئلهی تصمیمگیری آسانتر به نظر میرسد یا درواقع سختتر نیست. بهعنوانمثال ما میتوانیم مسئلهی کوتاهترین مسیر را حل کرده و تعداد لبهها را در کوتاهترین مسیر پیداشده با پارامتر k در مسئلهی تصمیمگیری مقایسه کنیم.
بهعبارتدیگر اگر یک مسئلهی بهینهسازی ساده باشد مسئلهی تصمیمگیری مرتبط با آنهم به همان نسبت ساده خواهد بود.
همچنین اگر دلایلی داشته باشیم که یک مسئلهی تصمیمگیری سخت است دلایلی خواهیم داشت که مسئلهی بهینهسازی مرتبط با آنهم سخت خواهد بود.
توضیح در مورد مفهوم کاهش
ایده ی نشان دادن اینکه یک مسئله سختتر یا آسانتر از مسئلهی دیگری نیست حتی زمانی که هر دو مسئله، مسئلهی تصمیمگیری باشند نیز به کار میرود. ما از این ایده تقریباً برای اثبات تمامی مسائل NPC استفاده میکنیم.
اجازه دهید یک مسئلهی تصمیمگیری مانند A را در نظر بگیریم که میخواهیم آن را در پیچیدگی زمانی چندجملهای O(nk) حل کنیم. ورودی را به یک مسئلهی خاص بهعنوان «نمونهای» از این مسئله فراخوانی میکنیم. بهعنوانمثال در مسئلهی مسیر، یک نمونه میتواند یک گراف خاص G باشد با دو رأس خاص u و v از G و مقداری مشخص برای پارامتر k. حال فرض میکنیم که یک مسئلهی تصمیمگیری دیگری داریم با نام B و میدانیم که این مسئله راهحلی در پیچیدگی زمانی چندجملهای دارد. درنهایت فرض میکنیم رویهای داریم که هر یک از نمونههای a از مسئلهی A را به نمونههای b از مسئلهی B با خصوصیات زیر تبدیل میکند یا «کاهش میدهد».
- عملیات کاهش دارای پیچیدگی زمانی چندجملهای است.
- جوابهای هر دو مسئله یکسان است؛ یعنی جواب مسئلهی a «بلی» است اگر و فقط اگر جواب مسئلهی b «بلی» باشد.
این رویه را الگوریتم کاهشی با پیچیدگی زمانی چندجملهای مینامیم که روشی را برای حل مسئلهی A در پیچیدگی زمانی چندجملهای فراهم میکند.
پس کلاً سه مرحلهداریم:
- نمونهی a از مسئلهی A را با استفاده از «الگوریتم کاهشی» با پیچیدگی زمانی چندجملهای به نمونهی b از مسئلهی B تغییر شکل میدهیم.
- الگوریتم کاهشی را بر روی نمونهی b از مسئله B اجرا میکنیم.
- از جوابی که برای b به دست آوردهایم بهعنوان جوابی برای مسئلهی a استفاده میکنیم.
تا زمانی که هر یک از این مراحل دارای پیچیدگی زمانی چندجملهای است هر سه مرحله باهم نیز دارای پیچیدگی زمانی چندجملهای خواهد بود و میتوانیم بگوییم که راهی با پیچیدگی زمانی چندجملهای برای تصمیمگیری روی مسئلهی a پیداکردهایم. بهعبارتدیگر با «کاهش» مسئلهی A به مسئلهی B، ما از سادگی B برای اثبات سادگی A استفاده کردهایم.
کلاس NP-complete زیر کلاس، کلاسهای NP و NP-hard است. درواقع کلاس NP-complete فصل مشترک کلاسهای NP و NP-hard را تشکیل میدهد. برای حل این مسائل هیچ الگوریتمی با پیچیدگی چندجملهای وجود ندارد.
مسئله M یک مسئله NP-complete است اگر و فقط اگر M یک مسئله NP-hard باشد و درعینحال M زیرمجموعه NP باشد.
چند نمونه مثال از مسائل NP-Complete
برخی از عبارتهای منطقی بهصورت ترکیبی عطفی نوشته میشوند. اینگونه عبارتهای منطقی یا یکبند هستند و یا ترکیب عطفی (AND) چند بند. میگوییم این عبارتها به شکل نرمال عطفی هستند. با علامت اختصاری CNF نشان داده میشوند. شکل نرمال عطفی درواقع همان شکل حاصلضرب مجموع هاست. ثابت میشود که ارضاء پذیری عبارتهای CNF یک مسئله NP-complete است. متعاقباً میتوان ثابت کرد که ارضاء پذیری خود به کلاس NP-complete تعلق دارد.
نمونه دیگری از مسائل NP-complete مسئله سه رنگپذیری است. اگر G یک گراف بدون جهت باشد مسئله سه رنگپذیری بررسی مینماید که آیا این گراف سه رنگپذیر هست یا خیر. آیا میشود گرههای گراف را با استفاده از تنها سه رنگ رنگآمیزی کرد که هیچ دو گره مجاور رنگ یکسانی نداشته باشند. چهار رنگپذیری گرافها نیز یک مسئله NP-complete است اما دورنگپذیری بک مسئله P است.
برای روشنتر شدن مفهوم این کلاس پیچیدگی به بررسی مسئله جمع زیرمجموعهها (Subset Sum Problem) میپردازیم. فرض کنید مجموعهای مانند {-7, -3, -2, 5, 8} شامل تعدادی عدد صحیح به ما داده شده است و هدف این است که زیرمجموعهای در آن یافت کنیم که جمع مؤلفههای آن برابر صفر شود. در مورد این مثال جواب مثبت است و زیرمجموعه {-3, -2, 5} بهعنوان جواب یافت میشود. به روال پیدا کردن اینکه آیا چنین زیرمجموعهای که جمع مؤلفههای صفر داشته باشد وجود دارد یا خیر، مسئله جمع زیرمجموعهها گفته میشود.
با بزرگ شدن طول مجموعه، تعداد زیرمجموعههای آن بهصورت نمایی رشد کرده و کار پیدا کردن جواب را مشکلتر میکند. به شکلی که این مسئله NP-Complete محسوب میشود. بههرحال اگر جواب را در دست داشته باشیم (که به آن اعتبارنامه نیز گفته میشود) بهراحتی میتوان مؤلفههای آن را جمع کرد و صفر بودن آن را تصدیق نمود؛ بنابراین اگر جمع زیرمجموعه ارائهشده برابر صفر باشد، آن زیرمجموعه بهعنوان اثبات یا شاهدی برای جواب مثبت به حقیقت ارائهشده است.
الگوریتمی که صحت صفر بودن جمع زیرمجموعه را تصدیق میکند، تصدیقکننده نام دارد. پس در تعریف خواهیم داشت که یک مسئله NP است اگر و فقط اگر برای آن تصدیقکنندهای وجود داشته باشد که جواب را در زمان چندجملهای تصدیق کند. پرواضح است که مسئله جمع زیرمجموعهها NP است.
نکتهای که باید به آن اشاره شود این است که در مورد تصدیق نشدن جواب در زمان چندجملهای تضمینی وجود ندارد. درواقع مسائلی که تصدیق نشدن آنها نیز در زمان چندجملهای صورت میگیرند مسائل co-NP نامیده میشوند.
لیست مسائل معروف NP-Complete
- SAT(مسئله رضایت بولی): مسئله تعیین درستی متغیرهای یک عبارت بولی به طوری که کل عبارت درست باشد.
- ۰-۱ INTEGER PROGRAMMING (برنامهنویسی خطی اعداد صحیح)
- CLIQUE یا independent set problem (مسئله گروهک یا مسئله مجموعه مستقل)
- SET PACKING (مسئله بستهبندی مجموعه)
- ورودی: خانوادهای از مجموعههای
 ، عدد صحیح مثبت k
، عدد صحیح مثبت k - ویژگی:
 شامل k مجموعه جدا از هم است.
شامل k مجموعه جدا از هم است.
- ورودی: خانوادهای از مجموعههای
- VERTEX COVER (مسئله پوشش رأس)
- ورودی: گراف G، عدد صحیح مثبت k
- ویژگی: زیرمجموعهای r عضوی از رئوس گراف وجود دارد که
 و حداقل یک طرف هر یال به عضوی از این زیرمجموعه میرسد.
و حداقل یک طرف هر یال به عضوی از این زیرمجموعه میرسد.
- SET COVERING (مسئله پوشش مجموعه)
- ورودی: خانوادهای محدود از مجموعههای محدود
 ، عدد صحیح مثبت k
، عدد صحیح مثبت k - ویژگی: یک زیرخانواده
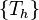 وجود دارد که زیرمجموعه
وجود دارد که زیرمجموعه  است و شامل کمتر یا مساوی k مجموعه است به طوری که
است و شامل کمتر یا مساوی k مجموعه است به طوری که 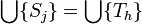
- ورودی: خانوادهای محدود از مجموعههای محدود
- FEEDBACK NODE SET (مسئله مجموعه رئوس پسخورد)
- FEEDBACK ARC SET (مسئله مجموعه یالهای پسخورد)
- DIRECTED HAMILTONIAN CIRCUIT (مسئله دور مستقیم همیلتونی)
- UNDIRECTED HAMILTONIAN CIRCUIT (مسئله دور غیرمستقیم همیلتونی)
- ۳SAT (مسئله ۳SAT)
- CHROMATIC NUMBER یا Graph Coloring Problem (مسئله عدد رنگی گراف یا مسئله رنگآمیزی گراف)
- CLIQUE COVER (مسئله پوشش گروهک)
- EXACT COVER (مسئله پوشش دقیق)
- HITTING SET (مسئله مجموعه ضربهزننده)
- STEINER TREE (مسئله درخت اشتاینر)
- ۳D MATCHING (مسئله تطابق سهبعدی)
- KNAPSACK یا Subset sum (مسئله کولهپشتی یا نسخه ی تصمیمی آن مسئله حاصلجمع زیرمجموعه)
- JOB SEQUENCING (مسئله ترتیبدهی شغل)
- PARTITION (مسئله تفکیک)
- MAX-CUT (مسئله بیشترین برش)
نتیجه گیری
مسائل NP در زمان نمایی با توجه به مقدار ورودی اجرا می شوند. واژه “NP کامل ” بدین معنی است که یک مسئله ارزش این را ندارد که سعی شود به صورت بهینه کامل حل شود.
منابع:
- Garey، M. and D. Johnson، Computers and Intractability; A Guide to the Theory of NP-Completeness، ۱۹۷۹. ISBN ۰-۷۱۶۷-۱۰۴۵-۵
- Cormen، Thomas H.; Leiserson، Charles E.; Rivest، Ronald L.; Stein، Clifford (۲۰۰۹). Introduction to Algorithms (۳rd ed.). MIT Press. ISBN ۰-۲۶۲-۰۳۳۸۴-۴.
- Richard M. Karp. “Reducibility Among Combinatorial Problems”. In Complexity of Computer Computations. R. E. Miller and J. W. Thatcher (editors). New York: Plenum, 1972. 85–103.















20 comments